Average bioequivalence study designs
The most common designs for bioequivalence studies are replicated crossover, nonreplicated crossover, and parallel. In a parallel design, each subject receives only one formulation in randomized fashion, whereas in a crossover design each subject receives different formulations in different time periods. Crossover designs are further broken down into replicated and nonreplicated designs. In nonreplicated designs, subjects receive only one dose of the test formulation and only one dose of the reference formulation. Replicated designs involve multiple doses. A bioequivalence study should use a crossover design unless a parallel or other design can be demonstrated to be more appropriate for valid scientific reasons. Replicated crossover designs should be used for individual bioequivalence studies, and can be used for average or population bioequivalence analysis.
In the Bioequivalence object, if all formulations have at least one subject given more than one dose of that formulation, then the study is considered a replicated design. For example, for the two formulations T and R, a 2x3 crossover design as described in the table below is a replicated crossover design.
|
|
Period 1 |
Period 2 |
Period 3 |
|
Sequence 1 |
T |
R |
T |
|
Sequence 2 |
R |
T |
R |
An example of a nonreplicated crossover design is the standard 2x2 crossover design described in the table below.
|
|
Period 1 |
Period 2 |
|
Sequence 1 |
T |
R |
|
Sequence 2 |
R |
T |
Information about the following topics is available:
•Recommended models for average bioequivalence
•Power of the two one-sided t-tests procedure
Recommended models for average bioequivalence
The default fixed effects, random effects, and repeated models for average bioequivalence studies depends on the type of study design: replicated crossover, nonreplicated crossover, or parallel.
Replicated data is defined as data for which, for each formulation, there exists at least one subject with more than one observation of that formulation. The default models depend on the type of analyses and the main mappings. For replicated crossover designs, the default model used in the Bioequivalence object is as follows:
Fixed effects model: Sequence + Formulation + Period
Random effects model: Subject(Sequence) and Type: Variance Components
Repeated specification: Period
•Variance Blocking Variables: Subject
•Group: Treatment
•Type: Variance Components
Nonreplicated crossover designs
Nonreplicated data is defined as data for which there exists at least one formulation where every subject has only one observation of that formulation. The default models depend on the type of analyses, the main mappings, and a preference called Default for 2x2 crossover set to all fixed effects (set under Edit > Preferences > LinMixBioequivalence). For nonreplicated crossover designs, the default model is as follows.
Fixed effects model: Sequence + Formulation + Period
•Unless the bioequivalence preference Default for 2x2 crossover set to all fixed effects is turned on in the Preferences dialog (Edit > Preferences > LinMixBioequivalence), in which case the model is Sequence + Subject(Sequence) + Formulation + Period.
Random effects model: Subject(Sequence) and Type: Variance Components
•Unless the bioequivalence preference Default for 2x2 crossover set to all fixed effects is turned on, in which case the model is not specified (the field is empty).
Repeated model is not specified.
Since there is no repeated specification, the default error model e ~ N(0, s2 I) is used. This is equivalent to the classical analysis method, but using maximum likelihood instead of method of moments to estimate inter-subject variance. Using Subject as a random effect this way, the correct standard errors will be computed for sequence means and tests of sequence effects. Using a fixed effect model, one must construct pseudo-F tests by hand to accomplish the same task.
Note:If Warning 11094 occurs, “Negative final variance component. Consider omitting this VC structure.”, when Subject(Sequence) is used as a random effect, this most likely indicates that the within-subject variance (residual) is greater than the between-subject variance, and a more appropriate model would be to move Subject(Sequence) from the random effects to the fixed effects model, i.e., Sequence+Subject(Sequence)+Formulation + Period.
When this default model is used for a standard 2x2 crossover design, Phoenix creates two additional worksheets in the output called Sequential SS and Partial SS, which contain the degrees of freedom (DF), Sum of Squares (SS), Mean Squares (MS), F-statistic and p-value, for each of the model terms. These tables are also included in the text output. Note that the F-statistic and p-value for the Sequence term are using the correct error term since Subject(Sequence) is a random effect.
If the default model is used for 2x2 and the data is not transformed, the intrasubject CV parameter is added to the Final Variance Parameters worksheet:
|
intrasubject CV=sqrt(Var(Residual))/RefLSM |
(1) |
where RefLSM is the Least Squares Mean of the reference treatment.
If the default model is used for 2x2 and the data is either ln-transformed or log10-transformed, the intrasubject CV and intrasubject CV parameters are added to the Final Variance Parameters worksheet:
•For ln-transformed data:
|
intersubject CV=sqrt(exp(Var(Sequence*Subject)) – 1) |
(2) |
|
intrasubject CV=sqrt(exp(Residual) – 1) |
(3) |
•For log10-transformed data:
|
intersubject CV=sqrt(10^(ln(10)*Var(Sequence*Subject)) – 1) |
(4) |
|
intrasubject CV=sqrt(10^(ln(10)*Var(Residual)) – 1) |
(5) |
Note that for this default model Var(Sequence*Subject) is the intersubject (between subject) variance, and Residual is the intrasubject (within subject) variance.
For parallel designs, whether data is replicated or nonreplicated, the default model is as follows.
Fixed effects model: Formulation
There is no random model and no repeated specification, so the residual error term is included in the model.
Note:In each case, users can supplement or modify the model to suit the analysis needs of the dataset. For example, if a Subject effect is appropriate for the Parallel option, as in a paired design (each subject receives the same formulation initially and then the other formulation after a washout period), set the Fixed Effects model to Subject+Formulation.
In determining the bioequivalence of a test formulation and a reference formulation, the first step is the computation of the least squares means (LSM) and standard errors of the test and reference formulations and the standard error of the difference of the test and reference least squares means. These quantities are computed by the same process that is used for the Linear Mixed Effects module. See “Least squares means” in the LinMix section.
To simplify the notation for this and the following sections, let:
•RefLSM: reference least squares mean,
•TestLSM: test least squares mean,
•fractionToDetect: (user-specified percent of reference to detect)/100,
•DiffSE: standard error of the difference in LSM,
•RatioSE: standard error of the ratio of the least squares means,
•df: degrees of freedom for the difference in LSM.
The geometric LSM are computed for transformed data. For ln-transform or data already ln-transformed,
|
RefGeoLSM=exp(RefLSM) |
(6) |
|
TestGeoLSM=exp(TestLSM) |
(7) |
For log10-transform or data already log10-transformed,
|
RefGeoLSM=10RefLSM |
(8) |
|
TestGeoLSM=10TestLSM |
(9) |
The difference is the test LSM minus the reference LSM,
|
Difference=TestLSM – RefLSM |
(10) |
The ratio calculation depends on data transformation. For non-transformed,
|
Ratio(%Ref)=100(TestLSM/RefLSM) |
(11) |
For ln-transform or data already ln-transformed, the ratio is obtained on arithmetic scale by exponentiating,
|
Ratio(%Ref)=100exp(Difference) |
(12) |
Similarly for log10-transform or data already log10-transformed, the ratio is
|
Ratio(%Ref)=100*10Difference |
(13) |
Output from the Bioequivalence module includes the classical intervals for confidence levels equal to 80, 90, 95, and for the confidence level that the user gave on the Options tab if that value is different than 80, 90, or 95. To compute the classical intervals, first the following values are computed using the students-t distribution, where 2*alpha=(100 – Confidence Level)/100, and Confidence Level is specified in the user interface.
|
Lower=Difference – t (1 – alpha),df*DiffSE |
(14) |
|
Upper=Difference + t (1 – alpha),df*DiffSE |
(15) |
These values are included in the output for the no-transform case. These values are then transformed if necessary to be on the arithmetic scale, and translated to percentages. For ln-transform or data already ln-transformed,
|
CI_Lower=100*exp(Lower) |
(16) |
|
CI_Upper=100*exp(Upper) |
(17) |
For log10-transform or data already log10-transformed,
|
CI_Lower=100*10Lower |
(18) |
|
CI_Upper=100*10Upper |
(19) |
For no transform,
|
CI_Lower=100*(1+Lower/RefLSM) = = |
(20) |
where the approximation RatioSE=DiffSE/RefLSM is used. Similarly,
|
CI_Upper=100 (1+Upper/RefLSM) |
(21) |
Concluding whether bioequivalence is shown depends on the user-specified values for the level and for the percent of reference to detect. These options are set on the Options tab in the Bioequivalence object. To conclude whether bioequivalence has been achieved, the CI_Lower and CI_Upper for the user-specified value of the level are compared to the following lower and upper bounds. Note that the upper bound for log10 or ln-transforms or for data already transformed is adjusted so that the bounds are symmetric on a logarithmic scale.
LowerBound=100 – (percent of reference to detect)
UpperBound (ln-transforms)=100 exp(–ln(1 – fractionToDetect))
=100 (1/(1 – fractionToDetect))
UpperBound (log10-transforms) =100*10^(–log10(1 – fractionToDetect))
=100 (1/(1 – fractionToDetect))
UpperBound (no transform)=100+(percent of reference to detect)
If the interval (CI_Lower, CI_Upper) is contained within LowerBound and UpperBound, average bioequivalence has been shown. If the interval (CI_Lower, CI_Upper) is completely outside the interval (LowerBound, UpperBound), average bioinequivalence has been shown. Otherwise, the module has failed to show bioequivalence or bioinequivalence.
For ln-transform or data already ln-transformed, the first t-test is a left-tail test of the hypotheses:
|
H0: true difference < ln(1 – fractionToDetect) (bioinequivalence for left test) |
(22) |
|
H1: true difference ³ ln(1 – fractionToDetect) (bioequivalence for left test) |
(23) |
The test statistic for performing this test is:
|
t1=((TestLSM – RefLSM) – ln(1 – fractionToDetect))/DiffSE |
(24) |
The p-value is determined using the t-distribution for this t-value and the degrees of freedom. If the p-value is <0.05, then the user can reject H0 at the 5% level, i.e. less than a 5% chance of rejecting H0 when it was actually true.
For log10-transform or data already log10-transformed, the first test is done similarly using log10 instead of ln.
For data with no transformation, the first test is (where Ratio here refers to the true ratio of the Test mean to the Reference mean):
|
H0: Ratio < 1 – fractionToDetect H1: Ratio ³ 1 – fractionToDetect |
(25) |
The test statistic for performing this test is:
|
t1=[(TestLSM/RefLSM) – (1 – fractionToDetect)]/RatioSE |
(26) |
where the approximation RatioSE=DiffSE/RefLSM is used.
The second t-test is a right-tail test that is a symmetric test to the first. However for log10 or ln-transforms, the test will be symmetric on a logarithmic scale. For example, if the percent of reference to detect is 20%, then the left-tail test is Pr(<80%), but for ln-transformed data, the right-tail test is Prob(>125%), since ln(0.8) = –ln(1.25).
For ln-transform or data already ln-transformed, the second test is a right-tail test of the hypotheses:
|
H0: true difference > –ln(1 – fractionToDetect) H1: true difference £ –ln(1 – fractionToDetect) |
(27) |
The test statistic for performing this test is:
|
t2=((TestLSM – RefLSM)+ln(1 – fractionToDetect))/DiffSE |
(28) |
For log10-transform or data already log10-transformed, the second test is done similarly using log10 instead of ln.
For data with no transformation, the second test is:
|
H0: Ratio > 1+fractionToDetect H1: Ratio £ 1+fractionToDetect |
(29) |
The test statistic for performing this test is:
|
t2=((TestLSM/RefLSM) – (1+fractionToDetect))/RatioSE |
(30) |
where the approximation RatioSE=DiffSE/RefLSM is used.
The output for the two one-sided t-tests includes the t1 and t2 values described above, the p-value for the first test described above, the p-value for the second test above, the maximum of these p-values, and total of these p-values. The two one-sided t-tests procedure is operationally equivalent to the classical interval approach. That is, if the classical (1 – 2 x alpha) x100% confidence interval for difference or ratio is within LowerBound and UpperBound, then both the H0s given above for the two tests are also rejected at the alpha level by the two one-sided t-tests.
Power of the two one-sided t-tests procedure
Power_TOST in the output is the power of the two one-sided t-tests procedure described in the previous section. Refer to the previous section for the definitions of t1 and t2 for the transformation that was used and recall from previous sections that df is the degrees of freedom for the difference of the test and reference least squares means. Define the critical t-value as:
|
|
(31) |
where 2a=(100 – Confidence Level/100) and Confidence Level is specified in the user interface.
In general:
|
Power of a test=1 – (probability of a type II error) |
(32) |
For the two one-sided t-tests procedure, H1 is bioequivalence (concluded when both of the one-sided tests pass) and H0 is nonequivalence. The power of the two one-sided t-tests procedure is (Phillips, K. F. (1990), or Diletti, E., Hauschke, D., and Steinijans, V. W. (1991)):
|
|
(33) |
This power is closely approximated by the difference of values from a non-central t-distribution (Owen, D. B. (1965)):
|
|
(34) |
This is the formula used in the Bioequivalence module (power is set to zero if this results in a negative), and the non-central t should be accurate to 1e–8. If it fails to achieve this accuracy, the non-central t-distribution is approximated by a shifted central t-distribution (again, power is set to zero if this results in a negative):
|
|
(35) |
Power of the two one-sided t-tests procedure is more likely to be of use with simulated data, such as when planning for sample size, rather than for drawing conclusions for observed data.
See Anderson and Hauck (1983), or page 99 of Chow and Liu (2000). Briefly, the Anderson-Hauck test is based on the hypotheses:
|
H01: H02: |
(36) |
where 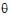 L and
L and 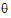 U are the natural logarithm of the Anderson-Hauck limits enter in the bioequivalence options tab. Rejection of both null hypotheses implies bioequivalence. The Anderson-Hauck test statistic is tAH given by:
U are the natural logarithm of the Anderson-Hauck limits enter in the bioequivalence options tab. Rejection of both null hypotheses implies bioequivalence. The Anderson-Hauck test statistic is tAH given by:
|
|
(37) |
where DiffSE is the standard error of the difference in means. Under the null hypothesis, this test statistic has a noncentral t-distribution.
Power_80_20 in the output is the power to detect a difference in least square means equal to 20% of the reference least squares mean. Percent of Reference to Detect on the Options tab should be the default value of 20%, and the desired result is that Power_80_20 is greater than 0.8 or 80%. (See pg. 142–143 of Chow and Liu (2000).) In general:
|
Power of a test=1 – (probability of a type II error) |
(38) |
Let 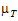 and
and 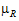 be the true (not observed) values of TestLSM and RefLSM. For this type of power calculation, for the no-transform case, the power is the probability of rejecting H0(
be the true (not observed) values of TestLSM and RefLSM. For this type of power calculation, for the no-transform case, the power is the probability of rejecting H0(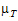 =
=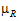 ) given H1:
) given H1:
|
| |
(39) |
For ln-transform, and data already ln-transformed, this changes to:
|
| |
(40) |
and similarly for log10-transform and data already log10-transformed.
For the default fractionToDetect=0.2, the default a=0.05 (2*a=(100 – Confidence_Level) /100), with no transform on the data and 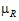 >0:
>0:
|
Power=Pr (rejecting H0 at the alpha level given the true difference in means=0.2* =Pr (| (TestLSM – RefLSM)/DiffSE | > ta,df |
(41) |
Let:
|
t1=t (1 – a),df – 0.2*RefLSM/DiffSE t2 = – t (1 – a),df – 0.2*RefLSM/DiffSE |
(42) |
Then:
|
Power » 1 – [Pr(T > t1) – Pr (T > t2)] |
(43) |
where T has a central t distribution with df=Diff_DF. Note that the second probability may be negligible.
For ln-transform or data already ln-transformed, this changes to:
|
t1=t (1 – a),df – (–ln(0.8))/DiffSE t2 = –t (1 – a),df – (–ln(0.8))/DiffSE |
(44) |
For the default parallel and 2x2 crossover models, some tests in Bioequivalence (e.g., the two one-sided t-tests) rely on the assumption that the observations for the group receiving the test formulation and the group receiving the reference formulation come from distributions that have equal variances, in order for the test statistics to follow a t-distribution. There are two tests in Bioequivalence that verify whether the assumption of equal variances is valid:
The Levene test is done for a parallel design that uses the default model (formulation variable with intercept included). See Snedecor and Cochran (1989) for more information.
The Pitman-Morgan test is done for a 2-period, 2-sequence, 2-formulation crossover design that uses either Variance Components or all fixed effects model. See Chow and Liu (2nd ed. 2000 or 3rd ed. 2009) for more information. In addition to the required column mappings, Sequence and Period must also be mapped columns.
For replicated crossover designs, the default model in Bioequivalence already adjusts for unequal variances by using Satterthwaite Degrees of Freedom and by grouping on the formulation in the repeated model, so a test for equality of variances is not done.
The results of the Levene test and Pitman-Morgan test are given in the Average Bioequivalence output worksheet and at the end of the Core Output. Both tests verify the null hypothesis that the true variances for the two formulations are equal by using the sample data to compute an F-distributed test statistic. A p-value of less than 0.05 indicates a rejection of the null hypotheses (and acceptance that the variances are unequal) at the 5% level of significance.
If unequal variances are indicated by the Levene or Pitman-Morgan tests, the model can be adjusted to account for unequal variances by using Satterthwaite Degrees of Freedom on the General Options tab and using a ‘repeated’ term that groups on the formulation variable as follows.
For a parallel design:
-
Map the formulation variable as Formulation.
-
Use the default Fixed Effects model (the formulation variable).
-
Use the default Degrees of Freedom setting of Satterthwaite.
-
Map the Dependent variable, and map the Subject and Period variables as Classification variables.
If the data does not contain a Period column, a column that contains all ones can be added as the Period variable. -
Set up the Repeated sub-tab of the Variance Structure tab as:
•Repeated Specification: Period
•Variance Blocking Variables (Subject): Subject
•Group: Formulation
•Type: Variance Components
For a 2x2 crossover design:
-
Map the Sequence, Subject, Period, Formulation, and Dependent variables accordingly.
-
Use the default model (Fixed Effects is Sequence+Formulation+Period, Random is Subject(Sequence)).
-
Use the default Degrees of Freedom setting of Satterthwaite.
-
Set up the Repeated sub-tab of the Variance Structure tab as:
•Repeated Specification: Period
•Variance Blocking Variables (Subject): Subject
•Group: Formulation
•Type: Variance Components
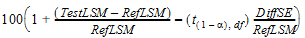
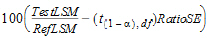
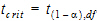
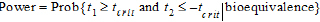
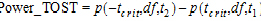
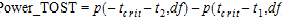
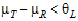
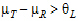
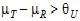
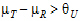
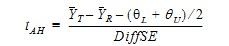
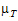 –
– 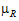 |=
|=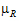
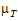 = –
= –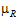 |= –ln(1 –
|= –ln(1 – 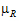 )
)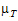 –
– 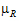 |=0.2*
|=0.2*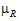 )
)